有哪些特殊矩阵？

通用的特殊矩阵

zeros函数 ：产生全0矩阵

 产生五行五列的随机矩阵A，其值是10--99的整数

产生均值0.6，方差0.1的五行五列正态矩阵B

 

产生五阶单位阵

验证等式成立

ones函数  ：产生全1矩阵

eye函数  ： 产生对角线为1的矩阵，当矩阵是方阵时，得到一个单位矩阵

rand函数  ：产生（0，1）区间分布的随机矩阵

randn函数  ：产生均值为0，方差为1的标准正态分布随机矩阵

 魔方矩阵（Magic Square）

三阶魔方阵

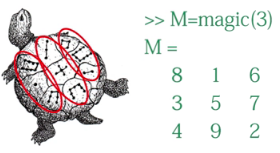
n阶魔方阵

n>2时，有很多不同的魔方阵，matlab中函数magic(n)只产生一个特定的魔方阵

例如，产生8阶魔方阵，求其每行每列元素之和

范德蒙矩阵

 希尔伯特矩阵

希尔伯特矩阵的元素为H(i,j)=1/(i+j-1)

生成希尔伯特矩阵的函数是hilb(n)

例如生成四阶希尔伯特矩阵,以有理数形式输出

希尔伯特矩阵是著名的病态矩阵，任何一个元素的值发生变动，整个矩阵和逆矩阵就会发生很大的变化

随着阶数的增加，病态越明显

伴随矩阵

 

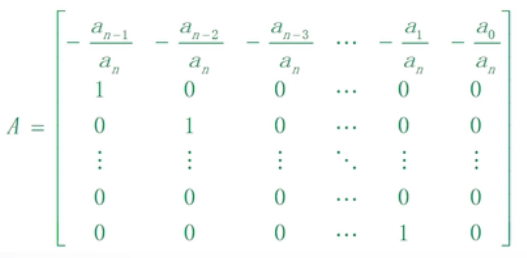
 生成伴随矩阵的函数是compan(p)

帕斯卡矩阵

生成5阶帕斯卡矩阵，整数形式输出

验证逆矩阵的所有元素也是整数